龟兔赛跑，floyd判圈算法

纸上得来终觉浅，绝知此事要躬行

算法推导

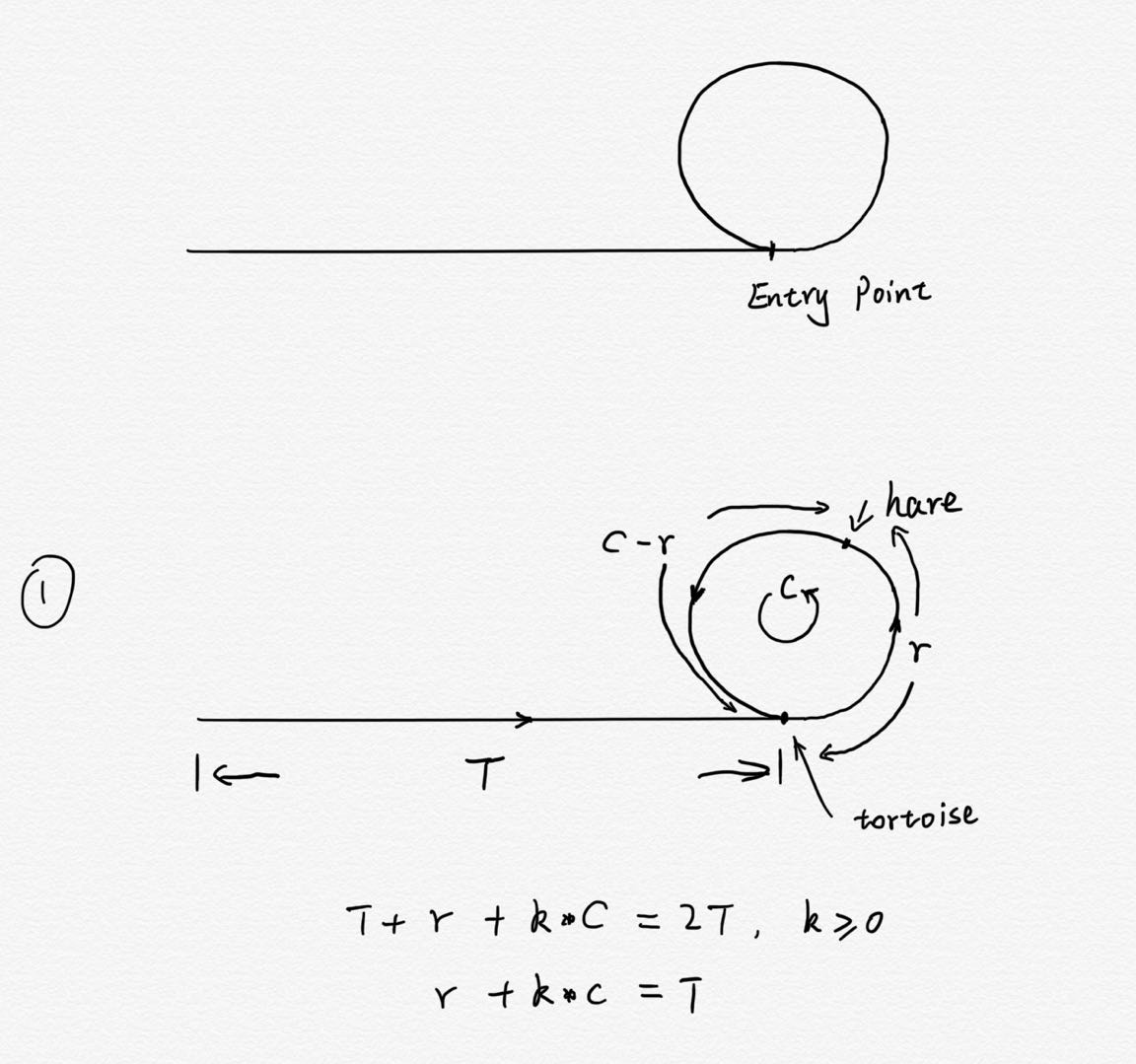
当hare的移动速度是tortoise的 2 倍，

设起始点到环的入口的距离是T，环的长度是C，

当tortoise第一次走到环的入口entry point时，我们假设这是tortoise与hare之间的在环上的距离是r，

从start point开始出发到tortoise第一次走到环的入口时，hare移动的距离是 T + r + k*C，k >= 0，

又因为，hare移动的速度是tortoise的两倍，且这时tortoise移动的距离是T，所以hare移动的距离是 2T。

得到等式 A T + r + k*C = 2T，k >= 0 简化得到等式 B r + k*C = T，k >= 0

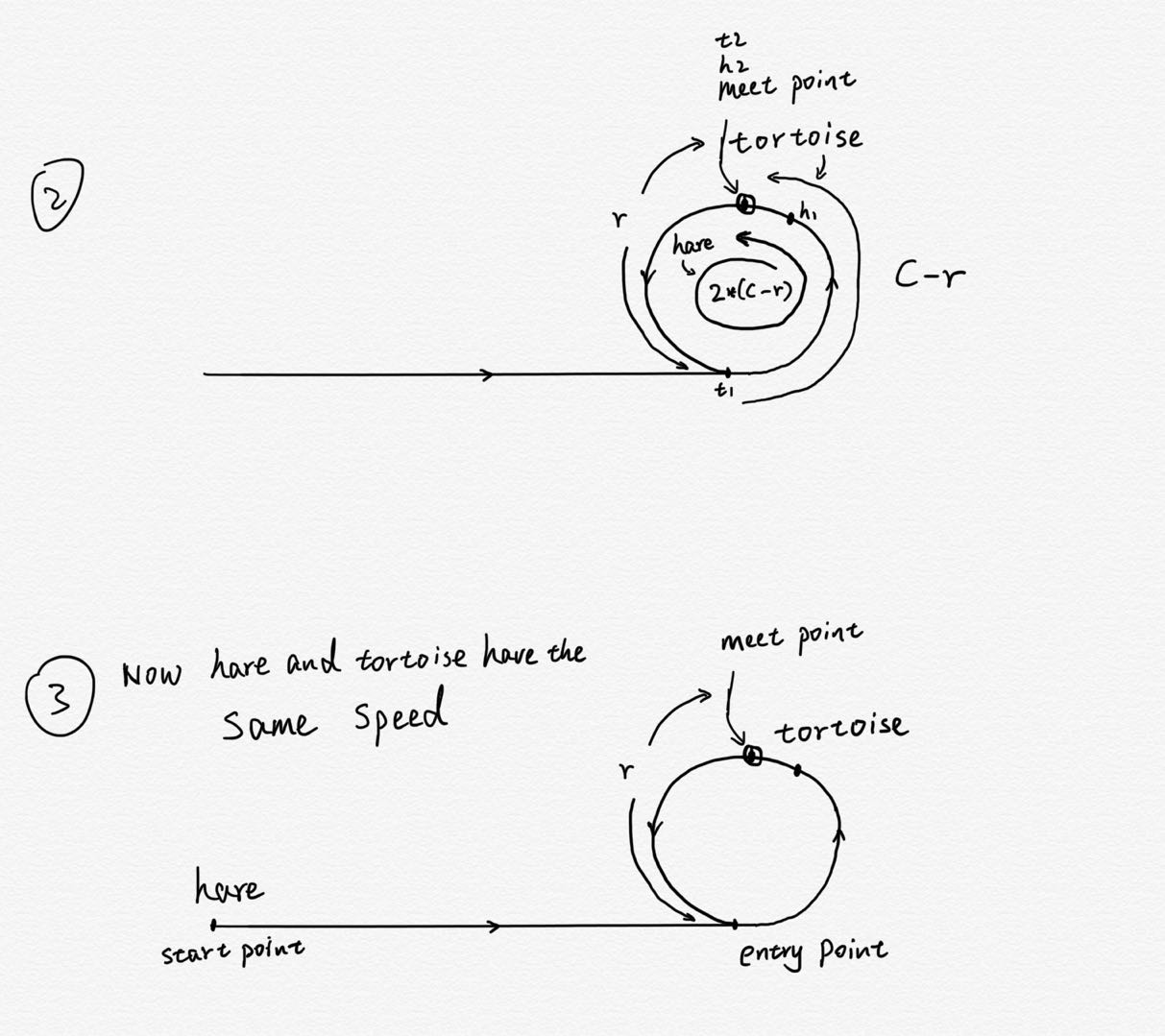
当 tortoise 第一次走到环的入口entry point时，而这时tortoise与hare之间的距离是 r，

那么如果tortoise现在就不继续移动的话，hare还需要往前走C-r才能追上tortoise。

但是hare在往前追赶tortoise的时候，tortoise也在移动，而hare的移动速度是tortoise的两倍，

所以hare可以追上tortoise,并且需要往前走2*（C-r）才能追上tortoise。

当hare移动了2*（C-r）的距离追上tortoise的时候，tortoise从相对于环的入口entry point移动了C-r。

所以，在tortoise与hare第一次在环上相遇时，环的入口entry point到这个点meet point的距离是C-r, 而从这个相遇点meet point再往前移动r，就又回到了环的入口entry point。

在hare与tortoise第一次相遇的这个时候，将hare从meet point重新放到起始点start point，tortoise仍放在这个相遇点meet point，

然后让它们以相同的速度开始移动，

根据等式 B r + k*C = T，k >= 0，

tortoise和hare必然会在环的入口点entry point再次相遇

入口entry point找到后，就能很容易得到T，

然后入口entry point，让tortoise停下，hare 继续跑一圈，就能得到 C。

算法应用

链表有环检测两个指针，慢指针移动速度为 1，快指针移动速度为 2，判断两个指针是否相遇
找出有环链表的入口节点当两个指针相遇时，将其中一个指针重新放到链表头，然后让两个指针移动速度都为 1，当两个指针再次相遇，就找到了有环链表的入口节点
计算环长度在入口节点放置两个个指针，一个指针不动，一个指针移动速度为 1，两个指针相遇，就可计算出环的长度

算法实现

golang

链表有环检测 leetcode 141

/*
 * @lc app=leetcode id=141 lang=golang
 *
 * [141] Linked List Cycle
 */

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func hasCycle(head *ListNode) bool {
	if head == nil {
		return false
	}
	t, h := head, head
	started := false
	for h != nil && h.Next != nil {
		if t == h {
			if started {
				return true
			} else {
				started = true
			}
		}
		t = t.Next
		h = h.Next.Next
	}
	return false
}

找出有环链表的入口节点 leetcode 142

/*
 * @lc app=leetcode id=142 lang=golang
 *
 * [142] Linked List Cycle II
 */

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func detectCycle(head *ListNode) *ListNode {
	var cycPoint *ListNode
	if head == nil {
		return cycPoint
	}
	t, h := head, head
	started := false
	hasCycle := false
	for h != nil && h.Next != nil {
		if t == h {
			if started {
				hasCycle = true
				break
			} else {
				started = true
			}
		}
		t = t.Next
		h = h.Next.Next
	}
	if hasCycle {
		h = head
		for h != nil && t != nil {
			if h == t {
				cycPoint = h
				break
			}
			h = h.Next
			t = t.Next
		}
	}
	return cycPoint
}

写在结尾

算法实现仔细想想就是初中做过的数学题目啊，哎，过了这么多年竟然忘的一干二净。